Discounted Payback Period
Discounted Payback Period Calculator (Click Here or Scroll Down)
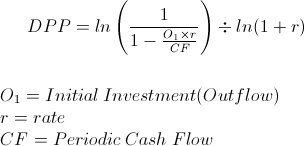
*Assumes cash flows are equal
**See below for simple and uneven cash flows version
The discounted payback period formula is used to calculate the length of time to recoup an investment based on the investment's discounted cash flows. By discounting each individual cash flow, the discounted payback period formula takes into consideration the time value of money.
The discounted payback period formula is used in capital budgeting to compare a project or projects against the cost of the investment. The simple payback period formula can be used as a quick measurement, however discounting each cash flow can provide a more accurate picture of the investment. As a simple example, suppose that an initial cost of a project is $5000 and each cash flow is $1,000 per year. The simple payback period formula would be 5 years, the initial investment divided by the cash flow each period. However, the discounted payback period would look at each of those $1,000 cash flows based on its present value. Assuming the rate is 10%, the present value of the first cash flow would be $909.09, which is $1,000 divided 1+r. Each individual cash flow would then be discounted to its present value until it is determined how long it would take to recoup the original $5,000.
Example of the Discounted Payback Period Formula
Using the prior example of a project that costs $5,000 with $1,000 annual cash flows. Assuming the company uses a discount rate of 10%, the discounted payback period for this example would be calculated based on the following equation:
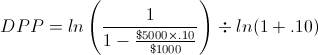
The equation for this example would be reduced to:
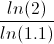
which results in a discounted payback period of 7.273. Although this formula calculates results with decimals, it is important to consider that there may be a slight difference due to rounding and more importantly, that there may not be a such thing as a partial cash inflow. This may warrant rounding up to determine how long it would take to recoup the initial investment.
Alternative Discounted Payback Period Formula
The formula listed at the top of the page assumes that each cash flow is equal. In many cases, the cash flows will not be equal. The simple version of the discounted payback period formula is:
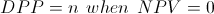
This is not as much a formula, as a way of explaining that the discounted cash flow method discounts each inflow until net present value equals zero.
Another method to simplify the calculation when cash flows are even is to use a table for the present value of annuity factor in order to solve n. The need to solve for n in the present value of annuity formula will be further explained in the following section.
How is the Discounted Payback Period Derived?
The formula shown at the top of the page assumes that all cash flows are equal. If all cash flows are equal, then the investment return is simply an annuity. The point of the discounted payback period formula is to calculate how long before the present value equals the initial investment(NPV = 0). Thus, since PV of the annuity equals the initial investment, solving for n, the number of periods, based on the present value of annuity formula can be used. The only difference between solving for n based on the PV of annuity formula and the formula shown at the top of the page is substituting PV for the initial investment since they are both equal.
As stated in the prior section, the process of calculating the discounted payback period when all cash flows are equal could be simplified by using a present value of annuity table to calculate n.
If the cash flows are uneven, then the longer method of discounting each cash flow would be used.
- Formulas related to Discounted Payback Period
- Net Present Value
- Equivalent Annual Annuity
- Payback Period
- Annuity (PV) - Solve for n
- Profitability Index