Interest Rate Parity
Interest Rate Parity Calculator (Click Here or Scroll Down)
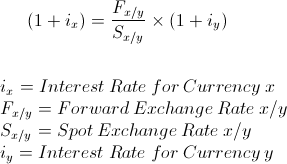
The formula for interest rate parity shown above is used to illustrate equilibrium based on the interest rate parity theory. The theory of interest rate parity argues that the difference in interest rates between two countries should be aligned with that of their forward and spot exchange rates.
When these variables do match, they are considered to be in equilibrium. When there is disequilibrium, an opportunity for arbitrage exists. Arbitrage is the buying and selling of goods, investments and/or currencies between two markets in order to profit from one market having a more favorable price. See the sections below that illustrate the differences of when there is equilibrium and disequilibrium.
* Two important considerations:
1. Theoretically, the rates should have the same risk. If one rate has a risk premium due additional risk, this would not be an equal comparison.
2. In practice, there is additional considerations such as fees, tax consequences, time, et cetera.
Example of the Interest Rate Parity Formula
An example of interest rate parity would be to suppose that the current exchange rate, or spot exchange rate, between the US and another country is $1.2544/1.00. Suppose that the US has an interest rate of 4% and the second country has a rate of 2%.
Using these variables, we can divide both sides of the equation by one plus the second country's interest rate, .02. This is shown as
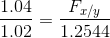
Both sides would need to be equal for there to be interest rate parity. The left side is equal to 1.0196. To find the forward exchange rate needed for equilibrium, both sides can then be multiplied by the spot exchange rate which is shown as
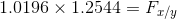
This would result in a forward rate of $1.279/1.00. This can be checked by using the interest rate parity calculator at the bottom of the page. Any other forward rate would show disequilibrium and the possibility of arbitrage.
Different variables can be known at different times and the formula can be rearranged to solve for the missing variable. For example, the local rate may be what is calculated for if the spot rate, forward rate, and foreign interest rate is known.
It is also important to consider that only 4 decimal places were used for this example. This was just to show an example. In practice, when large amounts of money are on the line, it is important to be precise, to not round, and use every decimal place of information available.
Use of the Interest Rate Parity Formula
The interest rate parity formula may be used by investors looking for arbitrage opportunities. More broadly speaking, global investors may be looking for the best investments across many economies and need a way to compare the various options. This entails considering how currencies may change in value, in respect to other currencies. Making a great return in a currency that has lost a great amount of value does not work out well, in sum.
- Formulas related to Interest Rate Parity
- Purchasing Power Parity