FV - Continuous Compounding
Future Value Continuous Compounding Calculator (Click Here or Scroll Down)
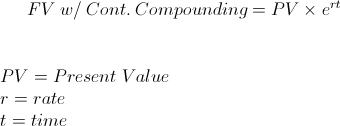
The future value with continuous compounding formula is used in calculating the later value of a current sum of money. Use of the future value with continuous compounding formula requires understanding of 3 general financial concepts, which are time value of money, future value as it applies to the time value of money, and continuous compounding.
Time Value of Money, Future Value, and Continuous Compounding
Time Value of Money - The future value with continuous compounding formula relies on the underlying concept of time value of money. Time value of money is the notion that a current sum of money(or unit of account) is worth more today than the same amount at a future date.
Future Value - Future value expands upon the idea of time value of money in that it quantifies the amount required at a later date. For example, suppose that an individual has a choice between receiving $1000 today or $1050 one year from today. Is the additional $50 worth waiting one year for? Can the individual invest elsewhere and make a higher return? Could the individual use the $1000 now for a higher "utility of enjoyment" than the $50 warrants? The future value with continuous compounding formula calculates the later value when there is continuous compounding.
Continuous Compounding - Continuous compounding is compounding that is in constant motion as opposed to incremental steps. Continuous compounding is considered to have an infinite amount of compounding periods for a certain period of time because there is no incremental steps as found in monthly or annual compounding.
Particularly the last 2 of these concepts lends to the actual formula for future value with continuous compounding.
Example of FV with Continuous Compounding Formula
An example of the future value with continuous compounding formula is an individual would like to calculate the balance of her account after 4 years which earns 4% per year, continuously compounded, if she currently has a balance of $3000.
The variables for this example would be 4 for time, t, .04 for the rate, r, and the present value would be $3000. The equation for this example would be
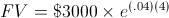
which return a result of $3520.53.
- Formulas related to FV with Continuous Compounding
- PV - Continuous Compounding
- Future Value
- Continuous Compounding