Doubling Time - Simple Interest
Doubling Time - Simple Interest Calculator (Click Here or Scroll Down)
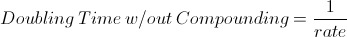
The doubling time for simple interest is simply 1 divided by the periodic rate. The formula for doubling time with simple interest is used to calculate how long it would take to double the balance on an interesting bearing account that has simple interest.
Simple interest is interest earned based solely on the principle. In contrast, compound interest is interest earned on principle along with prior interest earned.
Example of Doubling Time with Simple Interest
Suppose that an individual has a simple interest account at a rate of 10% per year with an original balance of $1000. This individual would like to determine how long before they would have $2000 in the account, double the amount of the original balance. For this intellectual exercise, we must assume that there are no deposits, fees, withdrawals, or other interferences.
For this example, the formula would simply be 1 divided by .10, which is the same as stating 10%. This would result in a doubling time of 10 years.
Notice that the original balance does not affect the time to double. However, the original balance would have an affect on an account that is compounded as interest is earned on prior interest earnings and the original balance would affect prior interest earnings.
**Again, it is worth noting that this formula applies to financial theory for unencumbered accounts. This is for educational purposes and real results may vary depending on fees and for other reasons.
How is Doubling Time with Simple Interest Formula Derived?
The doubling time formula for accounts with simple interest can be found by first looking at the simple interest formula used to calculate the ending balance:
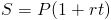
The ending balance would need to be twice as large as the original principle balance, so we would set S/P = 2:

From here, one can be subtracted by both sides which would show:
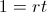
We are solving for time, or t, so both sides can be divided by the rate which will show the formula shown at the top of the page.
- Formulas related to Doubling Time - Simple Interest
- Simple Interest
- Doubling Time
- Doubling Time - Cont. Compounding