Annuity Due Payment - PV
Annuity Due Payment (PV) Calculator (Click Here or Scroll Down)
 1.gif)
The annuity due payment formula using present value is used to calculate each installment of a series of cash flows or payments when the first installment is received immediately. This particular formula uses the present value of the cash flows to calculate the payment.
Using present value versus using future value to calculate the payments on an annuity due depends on the situation. For example, if an individual is wanting to calculate the amount needed to save per year, starting today, in order to have a balance of $5000 after 5 years in an interest account, then the future value version would be used as $5,000 is the future value. This balance for this example would be increasing until it reaches the future value. However, the annuity due payment formula using present value would be used in situations where the balance is decreasing such as a periodic payout of the existing balance in an interest account.
Example of the Annuity Due Payment Formula Using Present Value
An example of the annuity due payment formula using present value would be an individual who would like to calculate the amount they can withdraw once per year in order to allow their savings to last 5 years. Suppose their current balance, which would be the present value, is $5,000 and the effective rate on the savings account is 3%.
It is important to remember that the individual's balance on their account will reach $0 after the 4th year or more specifically, the beginning of the 5th year, however the amount withdrawn will last the entire year composing a total of 5 years.
The equation for the annuity due payment formula using present value for this example would be:
 2.gif)
After solving, the amount withdrawn once per year starting today would be $1059.97. Actual amounts may vary by a few cents due to rounding.
How is the Annuity Due Payment from Present Value Formula Derived?
In order to arrive at the annuity due payment formula using present value, first the present value of annuity due formula must be considered, which is:
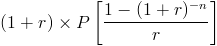
Since we are solving for the payment, P, the other portions of the formula can be factored out in order to solve for the payment, which resolves to the following formula:
 3.gif)
From here, the middle section of this formula can be reduced by multiplying the numerator, 1, by the inverse of the denominator which results in the formula shown at the top of the page.
- Formulas related to Annuity Due Payment (PV)
- Annuity Due Payment (FV)
- PV of Annuity Due
- Annuity Payment (PV)