Loan Payment
Loan Payment Calculator (Click Here or Scroll Down)
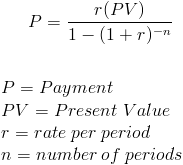
The loan payment formula is used to calculate the payments on a loan. The formula used to calculate loan payments is exactly the same as the formula used to calculate payments on an ordinary annuity. A loan, by definition, is an annuity, in that it consists of a series of future periodic payments.
The PV, or present value, portion of the loan payment formula uses the original loan amount. The original loan amount is essentially the present value of the future payments on the loan, much like the present value of an annuity.
It is important to keep the rate per period and number of periods consistent with one another in the formula. If the loan payments are made monthly, then the rate per period needs to be adjusted to the monthly rate and the number of periods would be the number of months on the loan. If payments are quarterly, the terms of the loan payment formula would be adjusted accordingly.
Standard Loan Payment
The loan payment formula shown is used for a standard loan amortized for a specific period of time with a fixed rate. Examples of specialized loans that do not apply to this formula include graduated payment, negatively amortized, interest only, option, and balloon loans.
An adjustable rate loan will use the formula shown but will need to be recalculated based on the remaining balance and remaining term for each new rate change.
Use of Loan Payment Formula
The loan payment formula can be used to calculate any type of conventional loan including mortgage, consumer, and business loans. The formula does not differ based on what the money is spent on, but only when the terms of repayment deviate from a standard fixed amortization.
Simple interest and amortized loans will generally have the same payment. The terms amortized and simple interest relate to how much of the payment is applied to principal and how much is applied to interest for each payment.
Simple interest loans rely on the date of payment to determine the amount of interest paid with the remaining amount going to principal. If a payment is made early, the interest portion of the payment will be less than if paid later. Less interest accrues when the amount is paid early because the loan balance will be less due to the extra principal payments.
On the other hand, an amortized loan has a predetermined amount of interest paid per payment so an earlier payment has no affect on lowering the principal balance sooner. Different companies and their loans will have different policies on how they are amortized. An example of how a company may amortize their loan, is by re-amortizing every year so that extra principal payments to the loan will only go in effect after a year to lower the monthly interest portions of the payment.
Alternative Loan Payment Formula
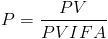
The payment on a loan can also be calculated by dividing the original loan amount (PV) by the present value interest factor of an annuity based on the term and interest rate of the loan. This formula is conceptually the same with only the PVIFA replacing the variables in the formula that PVIFA is comprised of.
- Formulas related to Loan Payment Formula
- Annuity Payment
- Loan - Remaining Balance
- Loan - Balloon Balance
Loan Payment Calculator
Actual payment may vary by institution due to rounding, fees, and other factors.
**It is important that the rate per period and number of periods match.
(e.g., If monthly, use the effective monthly rate.) See formula intro
section above for details**